Codes as Trees
Below is how both fixed-length and prefix-free binary codes can be viewed as binary trees, where each leaf corresponds to a codeword and each left edge is a $``0’’$ bit, each right edge is a $``1’’$ bit.
Fixed-Length Binary Codes
A fixed-length code over an $n$-symbol alphabet with codeword length $L = \lceil \log_2 n \rceil$ corresponds to a complete (full) binary tree of depth $L$. Every leaf sits exactly at depth $L$.
Example
Let $\Sigma = \lbrace A, B, C, D \rbrace$, then $L = 2$.
The tree may look like:

Paths:
| Symbol | Path | Codeword |
|---|---|---|
| A | left $\rightarrow$ left | 00 |
| B | left $\rightarrow$ right | 01 |
| C | right $\rightarrow$ left | 10 |
| D | right $\rightarrow$ right | 11 |
Since every leaf is at the same depth, decoding is trivial: just read 2 bits at a time.
Variable-Length Binary Codes
Any variable-length binary code can be represented by a proper binary tree in which:
- Every leaf corresponds to one symbol’s codeword.
- Because it’s prefix-free, no internal node is also a leaf — i.e. once you hit a leaf, you stop.
Example
Let’s take a small alphabet $\Sigma = \lbrace A, B, C, D \rbrace$ with weights that yield the Huffman codes:
| Symbol | Codeword |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
The corresponding tree looks like:
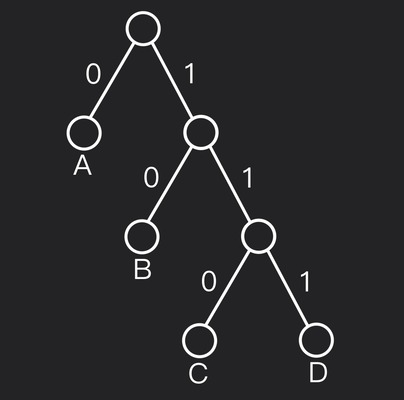
The depths of the leaves, reflecting their variable codeword lengths:
| Symbol | Depth |
|---|---|
| A | 1 |
| B | 2 |
| C | 3 |
| D | 3 |
Last updated 09 May 2025, 23:43 +0500 .