Huffman's Greedy Algorithm

Core Idea of Huffman’s Algorithm link

At its heart, Huffman’s algorithm is a greedy, bottom-up construction of an optimal prefix-free code. Here’s the intuition:

• Symbols as Weighted Leaves
  • Begin by treating each symbol $\sigma_i$ as a leaf node in a forest (a collection of one-node trees), labeled with its frequency $p_i$.
• Greedy Merge of the Least-Frequent
  • Always pick the two trees with the smallest total frequencies.
  • Merge them under a new parent node whose frequency is the sum of those two.
  • Repeat the $`` \text{extract two smallest } \rightarrow \text{ merge } \rightarrow \text{ reinsert}’’$ step until only one tree remains.
• Interpret the Tree as Codewords
  • Label each left‐edge $`` 0’’$ and each right‐edge $`` 1’’$.
  • The codeword for a symbol is simply the sequence of $0$’s and $1$’s along the path from the root to its leaf.

Why This Builds an Optimal Code link

Local Optimality → Global Optimality link

By always merging the two least-likely symbols, Huffman’s greedy step mimics the structure any optimal code must have: the two rarest symbols are siblings at maximum depth.

Optimal Substructure link

Once you merge two symbols, you’ve reduced the problem size by one — creating a new “super-symbol” whose frequency is the sum of its parts. Solving this smaller problem optimally and then unpacking the merges yields a globally optimal tree.

Visualization link

Suppose we have the symbols:

$$ \lbrace A,B,C,D,E\rbrace $$

and frequencies

$$ A:45,~ B:13,~ C:12,~ D:16,~ E:9 $$

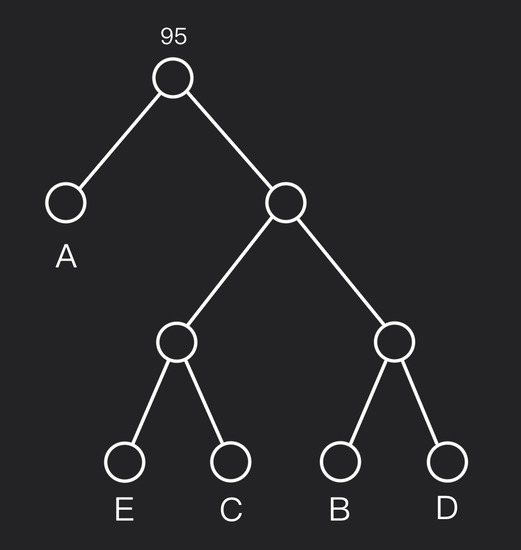
Step #1: Start with five one-node trees link

Each symbol is its own tree, weighted by its frequency.

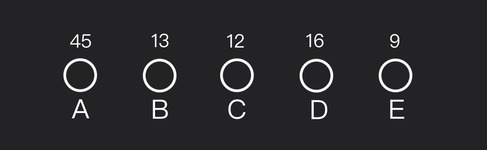
Step #2: Find the two smallest frequencies link

The smallest are $E(9)$ and $C(12)$. Merge them into a new subtree whose frequency is $9+12=21$.

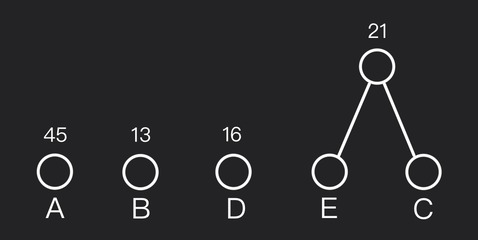
Step #3: Again pick the two smallest link

Now the forest has frequencies $13, 16, 21, 45$. The two smallest are $B(13)$ and $D(16)$. Merge into one node with frequency $13+16=29$.

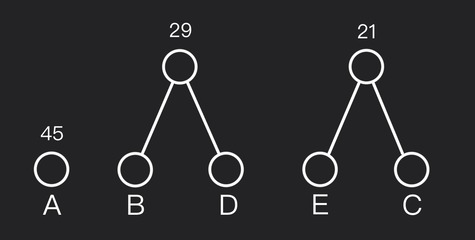
Step #4: Merge the next two smallest link

Forest frequencies are now $21, 29, 45$. Merge two trees with frequencies $21$ and $29$ into one node with frequency $21+29=50$.

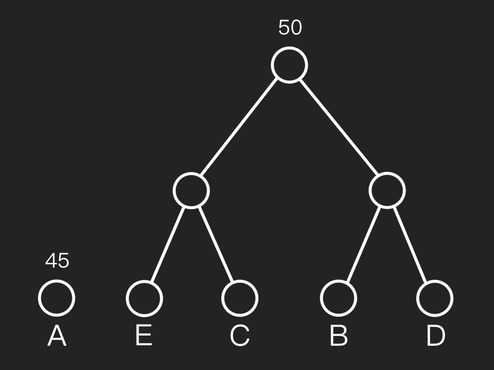
Step #5: Final merge to form the full tree link

Only two trees remain. Merge into the root, frequency $45+50=95$. This completes the Huffman tree.

Reading Off the Codewords link

So the final Huffman tree is:

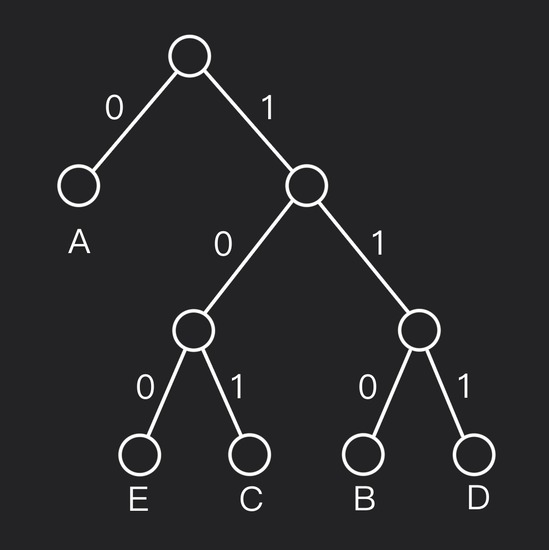
Follow the path from root to each leaf, writing down the bits:

• $A: ~ \text{left} \implies \text{code: 0}$
• $B: ~ \text{right} \rightarrow \text{right} \rightarrow \text{left} \implies \text{code: 110}$
• $C: ~ \text{right} \rightarrow \text{left} \rightarrow \text{right} \implies \text{code: 101}$
• $D: ~ \text{right} \rightarrow \text{right} \rightarrow \text{right} \implies \text{code: 111}$
• $E: ~ \text{right} \rightarrow \text{left} \rightarrow \text{left} \implies \text{code: 100}$

Average Code Length link

$$ L_{avg} = \sum_{\sigma \in \lbrace A,B,C,D,E \rbrace} p_\sigma \cdot l_\sigma \cdot \frac{45 \cdot 1 + 13 \cdot 3 + 12 \cdot 3 + 16 \cdot 3 + 9 \cdot 3}{95} \approx 2.05 ~ \text{bits/symbol} $$

This is the minimum possible average length for any prefix-free code on these frequencies.