Коды в виде деревьев
Ниже показано, как бинарные коды фиксированной длины и беспрефиксные коды могут быть представлены в виде двоичных деревьев, где каждый лист соответствует кодовому слову, левое ребро обозначает бит $``0’’$, а правое — бит $``1’’$.
Бинарные коды фиксированной длины
Код фиксированной длины над алфавитом из $n$ символов с длиной кодового слова $L = \lceil \log_2 n \rceil$ соответствует полному двоичному дереву глубины $L$. Каждый лист располагается ровно на уровне $L$.
Пример
Пусть $\Sigma = \lbrace A, B, C, D \rbrace$, тогда $L = 2$.
Дерево может выглядеть так:

Пути:
| Символ | Путь | Кодовое слово |
|---|---|---|
| A | влево $\rightarrow$ влево | 00 |
| B | влево $\rightarrow$ вправо | 01 |
| C | вправо $\rightarrow$ влево | 10 |
| D | вправо $\rightarrow$ вправо | 11 |
Поскольку все листья находятся на одной глубине, декодирование тривиально: достаточно читать по 2 бита за раз.
Бинарные коды переменной длины
Любой код переменной длины можно представить в виде корректного двоичного дерева, в котором:
- Каждый лист соответствует кодовому слову одного символа.
- Так как код беспрефиксный, ни одна внутренняя вершина не является листом — то есть при достижении листа декодирование завершается.
Пример
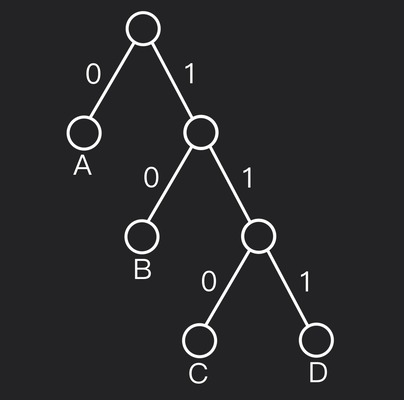
Рассмотрим алфавит $\Sigma = \lbrace A, B, C, D \rbrace$ с весами, дающими следующие коды Хаффмана:
| Символ | Кодовое слово |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
Глубины листьев:
| Символ | Глубина |
|---|---|
| A | 1 |
| B | 2 |
| C | 3 |
| D | 3 |
Last updated 09 мая 2025, 23:43 +0500 .