Жадный алгоритм Хаффмана
Основная идея алгоритма Хаффмана
В основе алгоритма Хаффмана лежит жадный, построенный «снизу вверх» подход к созданию оптимального беспрефиксного кода. Интуиция такова:
- Символы как взвешенные листья
- Сначала каждый символ $\sigma_i$ представляется в виде отдельного узла-дерева с весом, равным его частоте $p_i$.
- Жадное объединение наименее частотных
- На каждом шаге выбирайте два дерева с наименьшими суммарными частотами.
- Объединяйте их под общим узлом, чья частота равна сумме этих двух частот.
- Повторяйте шаг $\text{«извлечь два наименьших } \rightarrow \text{ объединить } \rightarrow \text{ вставить обратно»}$, пока не останется одно дерево.
- Интерпретация дерева как кодовых слов
- Обозначьте левое ребро как $\text{«} 0 \text{»}$, правое — $\text{«} 1 \text{»}$.
- Кодовым словом символа будет последовательность битов от корня до соответствующего листа.
Почему это даёт оптимальный код
Локальная оптимальность → глобальная оптимальность
Объединяя два наименее вероятных символа, жадный шаг воспроизводит структуру любого оптимального кода: два самых редких символа являются соседями на максимальной глубине.
Оптимальная подсоставная структура
После объединения двух символов задача уменьшается: появляется «супер-символ» с весом, равным сумме весов исходных символов. Оптимальное решение для уменьшенной задачи и обратная «распаковка» объединений дают оптимальное решение для исходной задачи.
Визуализация
Пусть имеется алфавит
$$ \lbrace A,B,C,D,E\rbrace $$
с частотами
$$ A:45,~ B:13,~ C:12,~ D:16,~ E:9 $$
Шаг №1: Начало с пяти одноузловых деревьев
Каждый символ — отдельное дерево с весом, равным его частоте.
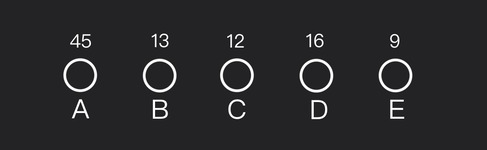
Шаг №2: Выбор двух наименьших
Минимальные частоты — $E(9)$ и $C(12)$. Объедините их в поддерево с суммарной частотой $9+12=21$.

Шаг №3: Снова два наименьших
Теперь лес содержит деревья с весами $13, 16, 21, 45$. Самые маленькие — $B(13)$ и $D(16)$. Объедините их в узел с весом $13+16=29$.
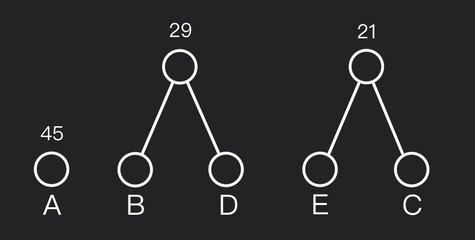
Шаг №4: Объединение следующих двух
Частоты леса — 21, 29, 45$. Объедините деревья с весами $21$ и $29$ в узел с весом $21+29=50$.
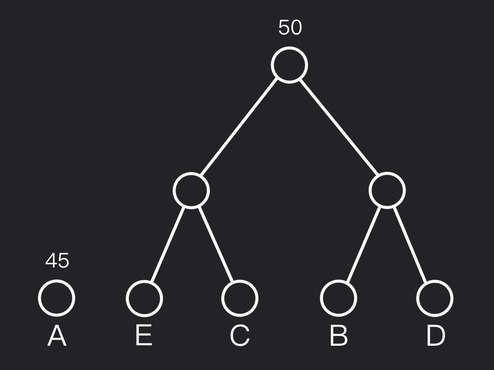
Шаг №5: Финальное объединение
Остаются два дерева с весами $45$ и $50$. Объедините их в корень с весом $45+50=95$. Это завершает построение дерева Хаффмана.
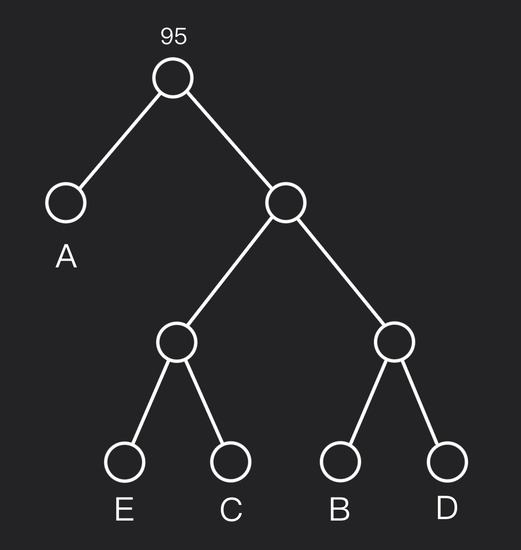
Извлечение кодовых слов
Итоговое дерево Хаффмана:
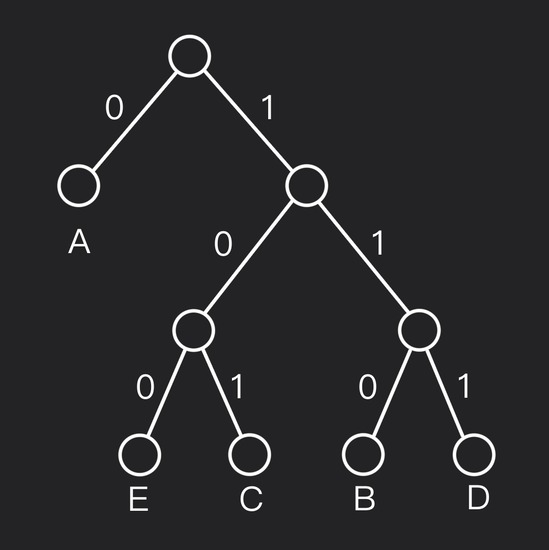
Путь от корня к листу даёт кодовое слово:
- $A: ~ \text{влево} \implies \text{code: 0}$
- $B: ~ \text{вправо} \rightarrow \text{вправо} \rightarrow \text{влево} \implies \text{code: 110}$
- $C: ~ \text{вправо} \rightarrow \text{влево} \rightarrow \text{вправо} \implies \text{code: 101}$
- $D: ~ \text{вправо} \rightarrow \text{вправо} \rightarrow \text{вправо} \implies \text{code: 111}$
- $E: ~ \text{вправо} \rightarrow \text{влево} \rightarrow \text{влево} \implies \text{code: 100}$
Средняя длина кода
$$ L_{avg} = \sum_{\sigma \in \lbrace A,B,C,D,E \rbrace} p_\sigma \cdot l_\sigma \cdot \frac{45 \cdot 1 + 13 \cdot 3 + 12 \cdot 3 + 16 \cdot 3 + 9 \cdot 3}{95} \approx 2.05 ~ \text{бит/символ} $$
Это минимально возможная средняя длина для любого беспрефиксного кода при заданных частотах.
Last updated 09 мая 2025, 23:43 +0500 .